Concours : les nombres autodigitaux

Rappel du problème paru dans le Virus 14 :
On dira d'un nombre qu'il est autodigital parfait s'il peut être calculé en utilisant tous les chiffres qui le compose dans leur ordre d'apparition (de gauche à droite). Si l'ordre d'apparition n'est pas respecté, on le dira imparfait. Un exemple valant mieux qu'un long discours :

Ces quatre nombres sont des autodigitaux parfaits. Le dernier nombre met en évidence qu'on accepte aussi, arbitrairement, d'utiliser des groupes de chiffres. Attention, on n'accepte pas d'utiliser le groupe formé de tous les chiffres, i.e. le nombre recherché lui-même, car cela manquerait un peu d'intérêt de constater que, par exemple, 660 = 660, non ? Les deuxième et troisième exemples montrent que l'opérateur de soustraction peut-être utilisé comme opérateur unaire (s'appliquant à une seule opérande), ce qui revient à dire qu'on accepte les nombres négatifs.

Dans le cadre de ce problème, on se limitera aux opérateurs suivant (que l'on pourra combiner autant que nécessaire) :

les quatres opérations de base : +, -, /, * (on accepte le "-" comme opérateur et comme signe)
l'élévation à la puissance : ^
la factorielle : ! [qui se définit par 0! = 1 ; 1! = 1 ; n! = 1 * 2 * ... * n (pour n > 1)]
la racine carrée :
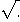
les parenthèses : ( )

Maintenant, saurez-vous faire un programme capable de trouver tous les nombres autodigitaux parfaits de 3 chiffres ? Bien sûr, si votre programme est capable de gérer plus d'opérateurs (la sommielle, pendant de la factorielle pour l'addition, ou le changement de base, ...) et qu'un nombre autodigital de n chiffres ne lui fait pas peur, il n'en laissera que d'avantage son empreinte.

Vous avez jusqu'à fin mars 2000 pour participer. Envoyez vos propositions et vos questions à David.

Contributions actuelles :
Pour l'instant le record, de 33 nombres autodigitaux parfaits entre 100 et 999, est détenu par Xavier Derlet.

Indice :
Voici un résultat de mathématique qui peut éventuellement servir pour simplifier certaines recherches :

Une factorielle n'est jamais un carré parfait.
(quelque soit l'entier m > 1, il n'existe pas d'entier n tel que n² = m!)

Démonstration : à venir... mais en gros, il faut passer par la décomposition en facteur premier et se servir d'un résultat sur la répartition des nombres premiers parmi les entiers (résultat que j'ai été bien incapable de démontrer jusqu'ici, mais qu'un mathématicien génial, Paul Erdös, a démontré à l'âge de 16 ans).

Vous voulez soutenir une information indépendante ? Rejoignez notre Club privé !

[homepage] [RSS] [archives]
[contact & legal & cookies] [since 1997]